
地震ではP波やS波が進んだときの速さや到着時刻などが問われる計算問題が出題されることが
あります。
このような計算問題では重要なポイントが2つあります。

P波やS波など地震に関する専門用語が出てくるので、難しい計算をしなければならないと思っ
てしまう人もいるかもしれません。
ですが心配いりません!
小学生のときから使ってきた次の速さの計算ができれば大丈夫です。

特に地震の計算ではP波やS波の速さを求める必要がある問題がほとんど。
はじめにP波やS波の速さを求めるようにしましょう。

初期微動継続時間とは、初期微動の続く時間のこと。
初期微動はP波によって引き起こされ、S波によってかき消されます。
そのため
初期微動継続時間=P波が到着してからS波が到着するまで
とも言えます。
よって
震源からの距離が2倍、3倍、4倍・・・
となると
初期微動継続時間も2倍、3倍、4倍・・・
となります。
また
震源からの距離:初期微動継続時間=常に一定の比
となるので、比例式をつくることもできます。


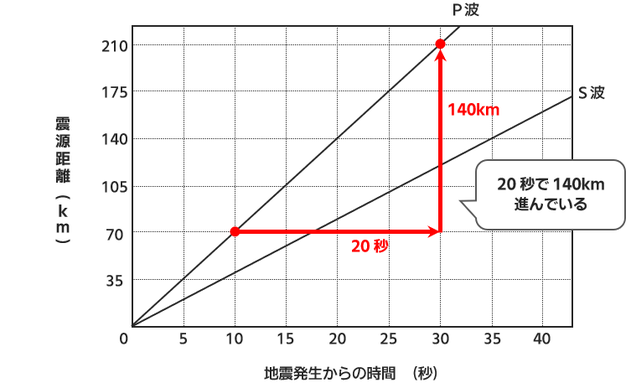
次のグラフは、ある地震における地震発生からの時間と震源からの距離の関係を表したもので
ある。

(1)P波の速さを求めよ。
(2)S波の速さを求めよ。
(3)震源から140kmの地点での初期微動継続時間を求めよ。
(4)震源から28kmの地点での初期微動継続時間を求めよ。
(解)
(1)「P波の速さを求めよ」
速さは

で求めます。
グラフから、P波は10秒で70km進んでいることが読み取れます。↓

よってその速さは

と求められます。
したがって答えは7km/秒です。
グラフのほかの数値を使ってもかまいません。↓
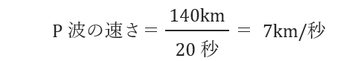
と求めても答えは同じです。
(2)「S波の速さを求めよ」
(1)と同様にして

で求めます。
グラフから、S波は35秒で140km進んでいることが読み取れます。↓

よってその速さは

と求めることができます。
したがって答えは4km/秒となります。
(3)「震源から140kmの地点での初期微動継続時間を求めよ」
初期微動継続時間はP波が到着してからS波が到着するまでの時間です。
グラフで、震源から140kmのところをチェックします。
P波が到着したのが20秒後。
S波が到着したのが35秒後。↓

したがって
初期微動継続時間=35秒-20秒=15秒
となります。
よって答えは15秒です。
(4)「震源から28kmの地点での初期微動継続時間を求めよ」
(3)と同じように、グラフで「震源から28km」を読み取りたいところ。
しかしグラフの「震源から28km」の位置にはメモリがないので正確に読み取ることができません。
そのような場合は
震源からの距離:初期微動継続時間=常に一定の比
を使います。
(3)より、震源から140kmの地点での初期微動継続時間が15秒とわかっているので
震源からの距離:初期微動継続時間=140km:15秒
です。
震源から28kmの地点での初期微動継続時間をx(秒)とすると
140km:15秒=28km:x(秒)
の比例式がつくれます。
これを解いて
x=3秒
となります。


次の表は、ある地震におけるA地点・B地点でのP波・S波の到着時刻をまとめたものである。

(1)P波の速さを求めよ。
(2)地震発生時刻を求めよ。
(3)A地点の初期微動継続時間を求めよ。
(解)
(1)「P波の速さを求めよ」
表のような形式で条件が与えられた問題は、表の条件を図にまとめるとわかりやすいです。
震源とA地点・B地点が一直線上にあるとしましょう。↓(※実際の震源は地下深くにあります)

ここに距離の情報を追加します。↓

さらにP波の到着時刻の情報を追加します。↓

このことから
P波は8秒間で60km進んでいる
ことがわかります。↓

よってその速さは

したがって答えは、7.5km/秒となります。
(2)「地震発生時刻を求めよ」
(1)で描いた図と、求めたP波の速さ7.5km/秒を利用します。
P波は震源を出発し、A地点やB地点に到着します。
特に震源からA地点までに注目。
P波は120kmの距離を7.5km/秒で進んでいることがわかります。

その際にかかった時間は
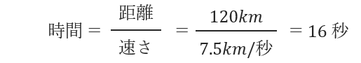
と求められます。
すなわちP波は
・震源を出発してから16秒後にA地点に到着
・A地点での到着時刻は15時12分50秒
したがって地震発生時刻は15時12分50秒の16秒前の
15時12分34秒となります。
(3)「A地点の初期微動継続時間を求めよ」
先述の通り、
初期微動継続時間は、P波が到着してからS波が到着するまでの時間。
表からA地点では
・P波は15時12分50秒に到着
・S波は15時13分04秒に到着
よって初期微動継続時間は
15時13分04秒 - 15時12分50秒 = 14秒
とわかります。
・はじめにP波やS波の速さを求めておこう。
・初期微動継続時間は、P波が到着してからS波が到着するまで。
・初期微動継続時間は震源からの距離に比例する。
・「震源からの距離:初期微動継続時間」は、常に一定の比になる。
次回は「災害とその対策」です!

