1.滑車を使った仕事
●定滑車
天井や壁、床などに固定されて動かない滑車。
●動滑車
天井や壁、床などに固定されておらず動くことのできる滑車。
例題1
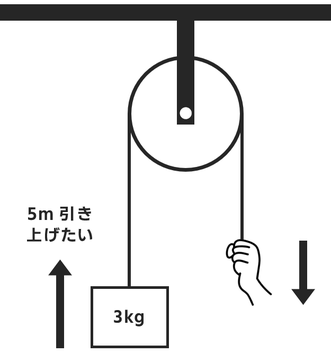
下の図のように3kgの物体を定滑車につるした。
糸の一端を手で引き、物体を5m持ち上げたい。
このとき、あとの問いに答えなさい。
ただし摩擦や空気抵抗は考えないものとする。
(1)糸を何Nの力で引けばよいか。
(2)糸を何m引けばよいか。
(3)手がした仕事は何Jか。
【解答】
3kgの物体にはたらく重力は30Nです。
つまり糸を30Nの力で引くと、3kgの物体を持ち上げることができます。

また糸を何m引くかは、物体を引き上げる長さに等しいはず。
(物体を引き上げたい分だけ、糸を引かなければならないということ)
よって糸を5m引くわけです。
そして手がした仕事は
仕事(J) = 力(N) × 力の向きに動いた距離(m) = 30N×5m = 150J
となります。
したがって答えは
(1)30N (2)5m (3)150J
となります。
※(3)の別解
仕事とは、どれだけその物体のエネルギーを変化させたかを表します。
仕事(J)=エネルギーの変化量
この問いでは滑車を使って物体を持ち上げています。
物体が持ち上がるということは、物体の位置エネルギーが増加するということ。
位置エネルギーは次の公式で求められます。
位置エネルギー(J)=重さ(N)×高さ(m)
30Nの物体を5m持ち上げているので
位置エネルギー=30N×5m=150J
となり、物体の位置エネルギーが150J大きくなります。
よって
仕事=エネルギーの変化量=150J
と求めることもできます。
例題2
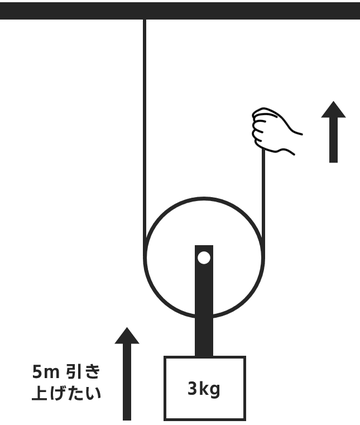
下の図のように3kgの物体を動滑車につるした。
糸の一端を手で引き、物体を5m持ち上げたい。
このとき、あとの問いに答えなさい。
ただし滑車の質量、摩擦や空気抵抗は考えないものとする。
(1)糸を何Nの力で引けばよいか。
(2)糸を何m引けばよいか。
(3)手がした仕事は何Jか。
【解答】
(1)
物体の質量は3kg。
そのため物体には30Nの重力がはたらいています。↓

この30Nの下向きの重力を天井と手の2か所で支えています。↓

そのため
天井が支える力(天井にはたらく力)=15N
手が支える力(手にはたらく力)=15N
となっています。
よって答えは15Nです。
(2)
物体を5m持ち上げるには、動滑車の左右両方のひもを5mずつ引き上げればよさそうです。
しかし片方のひもは固定されています。
つまり固定されているひもの分も、手で引かなければなりません。

式で書くと
5m×2=10m
よって正解は10mです。
(3)
(1)より、手が糸に加えた力は15N。
(2)より、手が糸を引いた長さは10m。
ここから
仕事(J) = 力(N) × 力の向きに動いた距離(m) = 15N×10m = 150J
よって仕事は150Jが正解です。
※(3)の別解
例題1の(3)の別解同様、30Nの物体が5m持ち上がり位置エネルギーが増加していることから、
増加した位置エネルギー=30N×5m=150J
よって150Jの仕事をした、と求めることもできます。
3.動滑車の特徴
例題1も例題2も「重さ30Nの物体を5m持ち上げる」という問題でした。
例題2のとき(動滑車を使ったとき)
手が引く力=15N
手が引く糸の長さ=10m
でした。
つまり動滑車を使うと
・手が引く力は1/2倍
・手が引く長さは2倍
となるのです。
しかし、しなければいけない仕事は変わりません。(例題1も例題2も150J)
このように道具を使っても使わなくても、仕事の量は変わりません。
このことを仕事の原理といいます。
・動滑車での仕事は・・・
→ 手が引く力は1/2倍・手が引く長さは2倍
→ でも仕事の量は変わらない。(仕事の原理)

