1.直列回路の抵抗の比
抵抗(電熱線)に流れる電流は同じであるため
「抵抗の比=電圧の比」
となる。
次のような直列回路を見てみましょう。(電源装置は省略)

この回路にI(A)の電流が流れ込んだとします。↓

このとき、
R₁の電流=I(A)
R₂の電流=I(A)
となります。↓

ここで「オームの法則」を思い出しましょう。
電圧(V)=抵抗(Ω)×電流(A)
オームの法則を用いることで
R₁の電圧=2Ω×I(A)=2I(V)
R₂の電圧=3Ω×I(A)=3I(V)
であることがわかります。↓

ここで条件をふり返ってみましょう。
▼抵抗の比
R₁の抵抗:R₂の抵抗=2:3
▼電圧の比
R₁の電圧:R₂の電圧=2I:3I=2:3
つまり直列回路では
抵抗の比=電圧の比
となるのです。
2.並列回路の抵抗の比
抵抗(電熱線)に加わる電圧は同じであるため
抵抗の逆比=電流の比
となる。
次のような直列回路を見てみましょう。(電源装置は省略)

この回路にE(V)の電圧を加えたとします。↓
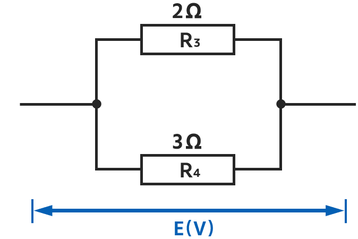
このとき、
R₃の電圧=E(V)
R₄の電圧=E(V)
となります。↓

ここで「オームの法則」を使いましょう。

ここから

であることがわかります。↓

ここで条件をふり返ってみましょう。
▼抵抗の比
R₃の抵抗:R₄の抵抗=2:3
▼電流の比

つまり並列回路では
抵抗の逆比=電流の比
となるのです。
例題
次のような回路でR₅・R₆・R₇に流れる電流をそれぞれ求めよ。

【解答】
解き方としては
①回路全体の抵抗(合成抵抗)を求める
②並列回路なので、「抵抗の逆比=電流の比」を使う
のどちらかとなります。
今回は②の比を使う考え方で解いてみましょう。
まず抵抗の比が
R₅の抵抗:R₆の抵抗:R₇の抵抗=4:2:8
です。
電流はその逆比なので

これをかんたんな整数比にすると
R₅の電流:R₆の電流:R₇の電流=2:4:1
となります。↓

つまり枝分かれ前は70mAだった電流が、2:4:1の割合で分かれていくのです。
よって

※R₇の電流は70mA-(20mA+40mA)=10mAと求めてもかまいません。
したがって正解は
R₅:20mA R₆:40mA R₇:10mA
となります。
直列回路・・・抵抗の比=電圧の比
並列回路・・・抵抗の逆比=電流の比

